Table des matières
Sortie d un Labyrinthe avec un mBot
Sortie d un Labyrinthe avec un mBot
Proposition de solution sortie Labyrinthe
Exemples
l_algorithme_de_pledge_-_interstices_-_interstices.pdf
idées d'algorythme pour sortir d un labytrinthe
- algolaby001.txt
Initialisation : *1 Démarrage du robot MBot. *2 Activation des capteurs de distance (Yeux). *3 Configuration des paramètres de vitesse et de détection. *Détection d'obstacle : *4 Si la distance est supérieure à 20 cm, le robot accélère. *5 Si la distance est entre 20 cm et 10 cm, le robot maintient une vitesse constante. *6 Si la distance est inférieure à 10 cm mais supérieure à 5 cm, le robot ralentit. *7 Si la distance est inférieure à 5 cm, le robot s'arrête. *Orientation pour trouver la sortie : *8 Si le robot est arrêté à cause d'un obstacle à 5 cm, il effectue une séquence d'orientations pour trouver la sortie. *9 Si après un virage à droite de 90°, il n'y a pas d'obstacle proche, le robot avance. *10 Sinon, s'il effectue un demi-tour (180°) et ne détecte pas d'obstacle proche, le robot avance. *11 Sinon, après un virage à gauche de 90°, le robot avance (car il aura effectué un demi-tour). *Répétition du processus : *12 Le robot continue à avancer tout en détectant les obstacles et ajustant sa vitesse en conséquence. *13 En cas d'obstacle à 5 cm, il effectue les étapes d'orientation pour trouver la sortie. *Fin : *14 Arrêt du robot lorsque la sortie du labyrinthe est détectée.
- algolaby00.txt
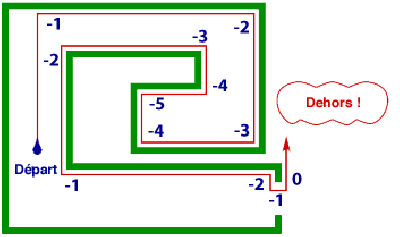
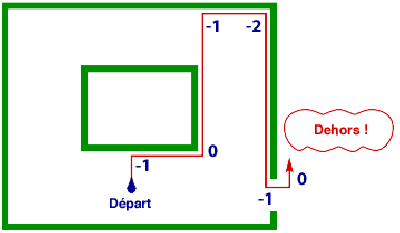
il ne suffit pas de marcher en ligne droite. Il faut compter les changements de direction. Supposons que, comme dans les exemples précédents, tous les angles soient droits. On n’a alors que deux possibilités, tourner à droite ou à gauche selon un angle de 90°. On compte les changements de direction en augmentant d’un point lorsque l’on tourne à gauche et en diminuant d’un point lorsque l’on tourne à droite (y compris la première fois que l’on tourne à droite quand on atteint un mur). Au début, le décompte est à zéro. Les deux instructions sont alors les suivantes : *1 Aller tout droit jusqu’au mur, passer à l’instruction 2 ; *2 Longer le mur par la droite (ou par la gauche, mais toujours dans le même sens) jusqu’à ce que le décompte des changements de direction atteigne zéro, passer à l’instruction 1 ; Il faut répéter ces actions jusqu’à ce que l’on revienne à la lumière du jour.
Algorithmes de sortie d un labyrinthe
Voici une présentation claire des principaux algorithmes de résolution de labyrinthe pour un robot, du plus simple au plus avancé. J’indique à chaque fois le principe, les avantages et les limites, avec un peu de pseudo-code quand c’est utile.
1. Algorithme de la (ou main gauche)
Principe
Le robot garde toujours la main droite en contact avec un mur. Tant que le labyrinthe est simplement connexe, il finira par trouver la sortie.
Avantages
- Très simple à implémenter
- Peu de mémoire
- Adapté aux robots simples (Arduino, capteurs IR)
Limites
- Ne fonctionne pas si le labyrinthe a des îlots (murs isolés)
- Pas forcément le chemin le plus court
Pseudo-code
tant que sortie non trouvée :
si mur à droite absent :
tourner à droite
avancer
sinon si devant libre :
avancer
sinon :
tourner à gauche
2. Algorithme de (marquage des chemins)
Principe
Le robot marque les passages déjà visités :
- 1 marque → déjà visité
- 2 marques → cul-de-sac
Il évite de repasser inutilement au même endroit.
Avantages
- Fonctionne dans tous les labyrinthes
- Garantit de trouver la sortie
Limites
- Besoin de mémoire (ou marquage physique)
- Plus complexe que la main droite
3.
Principe
Le robot explore un chemin jusqu’au bout, puis revient en arrière quand il est bloqué.
Avantages
- Simple conceptuellement
- Garantie de trouver la sortie
Limites
- Peut être très long
- Pas le plus court chemin
Pseudo-code simplifié
fonction DFS(case):
marquer case visitée
si case = sortie :
fin
pour chaque voisin libre :
si non visité :
DFS(voisin)
4.
Principe
Le robot explore niveau par niveau toutes les possibilités.
Avantages
- Trouve le plus court chemin
- Très fiable
Limites
- Utilise beaucoup de mémoire
- Moins adapté aux petits robots
5. * (A-star)
Principe
Algorithme intelligent utilisant :
- le coût déjà parcouru
- une estimation de la distance jusqu’à la sortie
Avantages
- Très rapide
- Chemin optimal
- Utilisé en robotique avancée
Limites
- Nécessite une carte du labyrinthe
- Plus complexe à programmer
6. Comparatif rapide
| Algorithme | Mémoire | Chemin optimal | Complexité |
|---|---|---|---|
| Main droite | Très faible | ❌ | Très simple |
| Trémaux | Faible | ❌ | Simple |
| DFS | Moyenne | ❌ | Moyenne |
| BFS | Élevée | ✅ | Moyenne |
| A* | Élevée | ✅ | Complexe |
Recommandation selon ton robot
- 🤖 Robot simple (capteurs, pas de carte) → Main droite ou Trémaux
- 🤖 Robot avec mémoire et carte → BFS ou A*
- 🤖 Projet scolaire → DFS ou Trémaux
Voici l’ajout de la gestion des angles et des virages précis pour un robot de labyrinthe avec capteurs IR / ultrasons, adapté à un robot à deux roues motrices (différentiel).
⚙️ Principe de base
Pour tourner proprement à 90°, le robot ne se contente pas d’un délai (delay) :
il utilise soit :
- ⏱️ le temps (solution simple)
- 🔄 les encodeurs de roues (précis)
- 🧭 un gyroscope (IMU) (très précis)
Je te montre les 3 niveaux, du plus simple au plus avancé.
🧩 Schéma de rotation du robot
Virage à 90° à droite
Vue de dessus
AVANT
↑
│
┌───┴───┐
│ ROBOT │ → rotation
└───┬───┘
│
↓
Roue gauche : AVANCE
Roue droite : RECULE (ou arrêt)
🟢 NIVEAU 1 – Rotation par le TEMPS (simple)
Schéma logique
Tourner à droite : - Moteur gauche : ON - Moteur droit : OFF - Temps ≈ 400 ms → 90°
Pseudo-code
void tournerDroite90() {
moteurGauche(AVANCE);
moteurDroit(ARRET);
delay(400); // à calibrer
arret();
}
✅ Avantages
- Très simple
- Suffisant pour projets scolaires
❌ Limites
- Dépend de la batterie et du sol
🟡 NIVEAU 2 – Rotation avec ENCODEURS (précis)
Principe
Chaque roue a un encodeur → nombre de ticks = angle.
Schéma
Angle = (ticks mesurés / ticks par tour) × 360°
Pseudo-code
void tournerDroite90() {
resetEncodeurs();
moteurGauche(AVANCE);
moteurDroit(RECULE);
while (encodeurGauche < TICKS_90) {
// attendre
}
arret();
}
✅ Avantages
- Bonne précision
- Indépendant du sol
🔵 NIVEAU 3 – Rotation avec GYROSCOPE (IMU)
Principe
Le robot mesure directement l’angle de rotation (yaw).
Schéma
Angle cible = angle actuel ± 90°
Pseudo-code
void tournerDroite90() {
float angleInitial = lireYaw();
moteurGauche(AVANCE);
moteurDroit(RECULE);
while (lireYaw() < angleInitial + 90) {
// rotation
}
arret();
}
✅ Avantages
- Très grande précision
- Utilisé en robotique avancée
🧭 Correction de trajectoire (ligne droite)
Schéma
Mur à droite trop proche → corriger à gauche Mur à droite trop loin → corriger à droite
Pseudo-code
erreur = distanceD - distanceConsigne; vG = vBase - Kp * erreur; vD = vBase + Kp * erreur;
👉 C’est un contrôle proportionnel (P).
🔄 Schéma global mis à jour
Lire capteurs
↓
Décision (droite / avant / gauche)
↓
Si virage :
→ rotation 90° précise
Sinon :
→ avance + correction mur
↓
Répéter
🧪 Conseils pratiques
- Calibrer les 90° une seule fois
- Utiliser encodeurs OU gyroscope si possible
- Toujours arrêter les moteurs après rotation
- Ajouter un petit délai de stabilisation (50 ms)
🎯 Résumé
| Méthode | Précision | Complexité |
|---|---|---|
| Temps | ⭐⭐ | ⭐ |
| Encodeurs | ⭐⭐⭐⭐ | ⭐⭐⭐ |
| Gyroscope | ⭐⭐⭐⭐⭐ | ⭐⭐⭐⭐ |
Voici un code Arduino COMPLET pour un robot résolveur de labyrinthe utilisant :
- 🧠 Algorithme : main droite
- 📏 Capteurs : ultrasons (HC-SR04) ou IR
- ⚙️ Virages précis à 90° par encodeurs (je t’indique aussi où adapter si tu n’as PAS d’encodeurs)
🧩 Matériel supposé
- Arduino UNO
- 2 moteurs DC + pont en H L298N
- 2 capteurs ultrasons (avant + droit)
- 2 encodeurs de roues
- Robot à 2 roues motrices
🔌 Connexions (exemple)
Moteurs (L298N)
ENA → pin 5 (PWM) IN1 → pin 6 IN2 → pin 7 ENB → pin 9 (PWM) IN3 → pin 10 IN4 → pin 11
Capteurs ultrasons
Avant : TRIG → 2 ECHO → 3 Droit : TRIG → 4 ECHO → 8
Encodeurs
Encodeur gauche → pin 18 (INT) Encodeur droit → pin 19 (INT)
⚙️ Constantes importantes
#define DIST_MUR 15 // cm #define VITESSE 150 #define TICKS_90 120 // À CALIBRER
🧠 CODE ARDUINO COMPLET
// ===== MOTEURS =====
#define ENA 5
#define IN1 6
#define IN2 7
#define ENB 9
#define IN3 10
#define IN4 11
// ===== ULTRASONS =====
#define TRIG_AV 2
#define ECHO_AV 3
#define TRIG_D 4
#define ECHO_D 8
// ===== ENCODEURS =====
volatile long ticksG = 0;
volatile long ticksD = 0;
#define DIST_MUR 15
#define VITESSE 150
#define TICKS_90 120
// ===== FONCTIONS ENCODEURS =====
void isrG() { ticksG++; }
void isrD() { ticksD++; }
// ===== SETUP =====
void setup() {
pinMode(ENA, OUTPUT);
pinMode(IN1, OUTPUT);
pinMode(IN2, OUTPUT);
pinMode(ENB, OUTPUT);
pinMode(IN3, OUTPUT);
pinMode(IN4, OUTPUT);
pinMode(TRIG_AV, OUTPUT);
pinMode(ECHO_AV, INPUT);
pinMode(TRIG_D, OUTPUT);
pinMode(ECHO_D, INPUT);
attachInterrupt(digitalPinToInterrupt(18), isrG, RISING);
attachInterrupt(digitalPinToInterrupt(19), isrD, RISING);
}
// ===== ULTRASON =====
long distanceCM(int trig, int echo) {
digitalWrite(trig, LOW);
delayMicroseconds(2);
digitalWrite(trig, HIGH);
delayMicroseconds(10);
digitalWrite(trig, LOW);
long duree = pulseIn(echo, HIGH, 20000);
return duree * 0.034 / 2;
}
// ===== MOTEURS =====
void avance(int v) {
digitalWrite(IN1, HIGH);
digitalWrite(IN2, LOW);
digitalWrite(IN3, HIGH);
digitalWrite(IN4, LOW);
analogWrite(ENA, v);
analogWrite(ENB, v);
}
void recule(int v) {
digitalWrite(IN1, LOW);
digitalWrite(IN2, HIGH);
digitalWrite(IN3, LOW);
digitalWrite(IN4, HIGH);
analogWrite(ENA, v);
analogWrite(ENB, v);
}
void stopMot() {
analogWrite(ENA, 0);
analogWrite(ENB, 0);
}
// ===== ROTATION PRECISE =====
void tournerDroite90() {
ticksG = 0;
ticksD = 0;
digitalWrite(IN1, HIGH);
digitalWrite(IN2, LOW);
digitalWrite(IN3, LOW);
digitalWrite(IN4, HIGH);
analogWrite(ENA, VITESSE);
analogWrite(ENB, VITESSE);
while (ticksG < TICKS_90) {}
stopMot();
delay(50);
}
void tournerGauche90() {
ticksG = 0;
ticksD = 0;
digitalWrite(IN1, LOW);
digitalWrite(IN2, HIGH);
digitalWrite(IN3, HIGH);
digitalWrite(IN4, LOW);
analogWrite(ENA, VITESSE);
analogWrite(ENB, VITESSE);
while (ticksD < TICKS_90) {}
stopMot();
delay(50);
}
// ===== BOUCLE PRINCIPALE =====
void loop() {
long dAvant = distanceCM(TRIG_AV, ECHO_AV);
long dDroit = distanceCM(TRIG_D, ECHO_D);
if (dDroit > DIST_MUR) {
tournerDroite90();
avance(VITESSE);
}
else if (dAvant > DIST_MUR) {
avance(VITESSE);
}
else {
tournerGauche90();
}
delay(20);
}
🔧 SI TU N’AS PAS D’ENCODEURS
Remplace les fonctions tournerDroite90() et tournerGauche90() par :
delay(400); // à calibrer
🧪 Calibration indispensable
- Tester un virage à 90°
- Ajuster
TICKS_90 - Ajuster
DIST_MUR(12–20 cm) - Ajuster
VITESSE
🎓 Résultat
✅ Le robot :
- suit le mur droit
- prend des virages précis
- sort du labyrinthe automatiquement
Parfait 👍 Voici un schéma électrique détaillé (texte + explications claires) pour ton robot résolveur de labyrinthe Arduino avec :
- Arduino UNO
- Pont en H L298N
- 2 moteurs DC
- 2 capteurs ultrasons HC-SR04
- 2 encodeurs de roues
- Alimentation batterie
🔋 1. Alimentation (TRÈS IMPORTANT)
Batterie 7–12V
+ -----------+
| |
| +--+--> L298N +12V
| |
| +--------> Arduino Vin
|
+------------------> GND commun
⚠️ Toutes les masses (GND) DOIVENT être communes
⚙️ 2. Pont en H L298N (moteurs)
Schéma logique
L298N
┌───────────────────┐
│ │
ENA──┤5 OUT1 ─── Moteur gauche +
IN1──┤6 OUT2 ─── Moteur gauche -
IN2──┤7
│
ENB──┤9 OUT3 ─── Moteur droit +
IN3──┤10 OUT4 ─── Moteur droit -
IN4──┤11
│
GND──┤GND
+12V─┤+12V
└───────────────────┘
Connexions Arduino → L298N
| Arduino | L298N |
|---|---|
| 5 (PWM) | ENA |
| 6 | IN1 |
| 7 | IN2 |
| 9 (PWM) | ENB |
| 10 | IN3 |
| 11 | IN4 |
| GND | GND |
📏 3. Capteurs ultrasons HC-SR04
Schéma capteur
HC-SR04 ┌──────────┐ │ VCC → 5V│ │ TRIG → Dx│ │ ECHO → Dx│ │ GND → GND│ └──────────┘
Connexions
Capteur AVANT
| HC-SR04 | Arduino |
|---|---|
| VCC | 5V |
| TRIG | D2 |
| ECHO | D3 |
| GND | GND |
Capteur DROIT
| HC-SR04 | Arduino |
|---|---|
| VCC | 5V |
| TRIG | D4 |
| ECHO | D8 |
| GND | GND |
🔄 4. Encodeurs de roues
Schéma simplifié
Encodeur ┌──────────┐ │ VCC → 5V │ │ GND → GND│ │ OUT → INT│ └──────────┘
Connexions
| Encodeur | Arduino UNO |
|---|---|
| Gauche OUT | D18 (INT) |
| Droit OUT | D19 (INT) |
| VCC | 5V |
| GND | GND |
⚠️ D18 et D19 = Arduino MEGA 👉 Si tu as UNO, utilise D2 et D3 (changer le code).
🧠 5. Schéma global (vue d’ensemble)
+--------------------+
| Arduino UNO |
| |
| D2 <--- TRIG AV |
| D3 <--- ECHO AV |
| D4 <--- TRIG D |
| D8 <--- ECHO D |
| |
| D5 ---> ENA L298N |
| D6 ---> IN1 |
| D7 ---> IN2 |
| D9 ---> ENB |
| D10 ---> IN3 |
| D11 ---> IN4 |
| |
| 5V ---> Capteurs |
| GND ---> GND COMMUN|
+--------------------+
|
|
+----+----+
| L298N |
+----+----+
|
Moteur G Moteur D
⚠️ Points critiques à respecter
✔ Masse commune partout ✔ Ne pas alimenter moteurs depuis le 5V Arduino ✔ Mettre le jumper ENA/ENB (ou PWM Arduino) ✔ Batterie assez puissante (≥ 1500 mAh)
🎓 Pour un rendu PRO (optionnel)
- Interrupteur général sur la batterie
- Condensateurs 100 nF sur moteurs
- Régulateur 5V externe (LM2596)
✅ Résumé
Ce schéma permet :
- contrôle précis des moteurs
- lecture fiable des capteurs
- virages à 90° propres
- robot stable et robuste
la version texte simulée des blocs mBlock
🟦 Programme principal – Capture simulée
+-----------------------------------------------------+ | [quand Arduino démarre] | | +---------------------------------------------+ | | | [répéter indéfiniment] | | | | +-------------------------------------+ | | | | | [mettre distance_avant à (ultrason D2/D3)] | | | | [mettre distance_droite à (ultrason D4/D8)] | | | | [si (distance_droite > SEUIL)] | | | | | +-------------------------------+ | | | | | | [tourner_droite_90] | | | | | | | [avancer] | | | | | | +-------------------------------+ | | | | | [sinon] | | | | | +-------------------------------+ | | | | | | [si (distance_avant > SEUIL)] | | | | | | | [avancer] | | | | | | | [sinon] | | | | | | [tourner_gauche_90] | | | | | +-------------------------------+ | | | | | [attendre 0.02 s] | | | | +-------------------------------------+ | | +---------------------------------------------+ | +-----------------------------------------------------+
✅ Correspondance logique
- Priorité à la droite
- Sinon, tout droit
- Sinon, tourner à gauche
- Boucle infinie, avec un petit délai pour stabilité
Pour ton robot suiveur de mur et résolveur de labyrinthe, la variable SEUIL représente la distance minimale (en cm) à laquelle le robot considère qu’il y a un mur. Elle dépend de :
- La portée de tes capteurs (IR ou ultrasons HC-SR04)
- La largeur du robot
- La vitesse et précision du robot
🔹 Valeurs typiques
| Capteur | SEUIL recommandé (cm) | Remarques |
|---|---|---|
| HC-SR04 (ultrasons) | 12 – 20 | 15 cm est un bon point de départ |
| Capteurs IR | 5 – 12 | IR détecte de plus près, car moins précis à longue distance |
🔹 Comment choisir la valeur exacte
- Commence par 15 cm si tu utilises des ultrasons.
Teste le robot dans ton labyrinthe :
- Si le robot percute les murs → augmenter le SEUIL
- Si le robot s’éloigne trop du mur → diminuer le SEUIL
- Ajuste petit à petit par pas de 1 ou 2 cm jusqu’à obtenir un suivi stable du mur.
🔹 Exemple pour mBlock
SEUIL = 15
distance_avant > SEUIL→ voie libre devantdistance_droite > SEUIL→ mur droit libre
Voici un mini guide visuel explicatif pour comprendre comment le robot utilise la variable SEUIL pour suivre les murs et décider de ses mouvements dans le labyrinthe.
🔹 Schéma explicatif : SEUIL et décisions
Mur avant
|
|
+------+------+
| |
| ROBOT |
| |
+------+------+
|
distance_avant
|
SEUIL ?
1️⃣ Lecture des distances
distance_avant→ mesure devant le robotdistance_droite→ mesure sur le côté droit
2️⃣ Comparaison avec SEUIL
| Capteur | Lecture < SEUIL | Lecture > SEUIL | Action du robot |
|---|---|---|---|
| Droite | Mur proche | Mur libre | Tourner à droite si libre |
| Avant | Mur proche | Voie libre | Avancer si libre |
3️⃣ Exemple de décision
Si distance_droite > SEUIL → tourner à droite puis avancer Sinon si distance_avant > SEUIL → avancer Sinon → tourner à gauche
4️⃣ Visualisation de l’espace autour du robot
Avant (distance_avant)
15 cm SEUIL
┌─────────────┐
Mur │ │ Mur
│ ROBOT │
│ │
└─────────────┘
Droite (distance_droite)
15 cm SEUIL
- Si droite > SEUIL → espace libre → priorité à droite
- Si avant > SEUIL → espace libre devant → avancer
- Sinon → mur devant et droite bloquée → tourner à gauche
✅ Résumé
- SEUIL = distance critique pour détecter un mur
- Plus le robot est rapide, plus SEUIL doit être grand
- Ce système simple permet au robot de sortir automatiquement du labyrinthe avec l’algorithme “main droite”